Page 122 - 机械工程材料2024年第十一期

李国强，等：基于多温度SDFF模型的反应堆压力容器钢韧脆转变区韧性评价

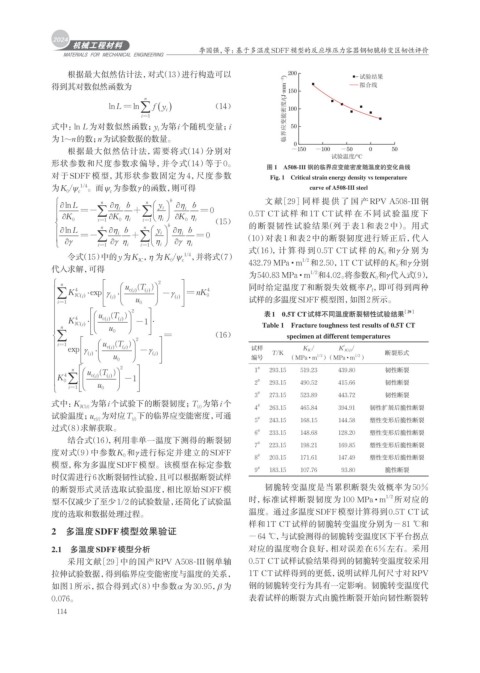
根据最大似然估计法，对式（13）进行构造可以 200 - 试验结果

得到其对数似然函数为 150 拟合线
n
ln L = ln ∑ f y i （14） 临界应变能密度/(J·mm -3 ) 100
( )
i =1
式中：ln L为对数似然函数； y i 为第i个随机变量； i 50

为1~n的数； n为试验数据的数量。
0
根据最大似然估计法，需要将式（14）分别对 -150 -100 -50 0 50
试验温度/℃
形状参数和尺度参数求偏导，并令式（14）等于 0。
图 1 A508-III 钢的临界应变能密度随温度的变化曲线
对于SDFF模型，其形状参数固定为 4，尺度参数 Fig. 1 Critical strain energy density vs temperature
为K /ψ 1/4 。而ψ 为参数γ 的函数，则可得 curve of A508-III steel
0 c c
 ln L n ∂ η ∂ b n  y  b ∂ η b 文 献［29］同样提供了国产 RPV A508-III钢
 =- ∑ i + ∑ i  i = 0
 K i ∂ K η∂ i i η i  ∂ K η 0 =1  i 0.5T CT试样和 1T CT试样在不同试验温度下
 0 =1 0 b （15） 的断裂韧性试验结果（列于表 1 和表 2 中）。用式
 ln L n ∂ η ∂ i b n  ∑ y  i ∂ η i b
 γ ∂ =- ∑ ∂ γ η + η  ∂ γ η = 0 （10）对表 1 和表 2 中的断裂韧度进行矫正后，代入
 i =1 i i =1  i  i
式（16），计算得到 0.5T CT 试样的K 0 和γ 分别为
令式（15）中的y为K ，η 为K /ψ 1/4 ，并将式（7）
JC 0 c 432.79 MPa · m 和2.50，1T CT试样的K 0 和γ 分别
1/2
代入求解，可得
1/2
为540.83 MPa · m 和4.02。将参数K 0 和γ 代入式（9），
 n   )T  u 2  同时给定温度T和断裂失效概率P f ，即可得到两种
 K 4 ⋅exp  γ ∑ ( )  ⋅ c ( ) i ( ( ) i  γ  = nK 4
 i JC ( ) i  i   u   - ( ) i  0 试样的多温度SDFF模型图，如图2所示。
 =1  0 
   ( )T  u 2  表1 0.5T CT试样不同温度断裂韧性试验结果 ［29］
 K JC ( ) i   c ( ) i ( ) i  -1  ⋅ ⋅ Table 1 Fracture toughness test results of 0.5T CT
4
   n  u    
∑ 0  = （16） specimen at different temperatures
i
 =1    c ( ) i ( ( ) i )T  u 2  
 exp γ ( )  i ⋅    - γ ( ) i 试样 T/K K JC / K' JC(t) / 断裂形式
    u 0    编号 （MPa · m ） （MPa · m ）
1/2
1/2
 n  2  #
 K 4 ∑   c ( ) i ( ( ) i )T  u  1 293.15 519.23 439.80 韧性断裂
 0      -1  2 # 293.15 490.52 415.66 韧性断裂
i =1   u 0   
#
3 273.15 523.89 443.72 韧性断裂
式中：K JC(i) 为第i个试验下的断裂韧度；T 为第i个 4 # 263.15 465.84 394.91 韧性扩展后脆性断裂
(i)
试验温度；u 为对应T 下的临界应变能密度，可通
c(i) (i) 5 # 243.15 168.15 144.58 塑性变形后脆性断裂
过式（8）求解获取。
6 # 233.15 148.68 128.20 塑性变形后脆性断裂
结合式（16），利用非单一温度下测得的断裂韧
7 # 223.15 198.21 169.85 塑性变形后脆性断裂
度对式（9）中参数K 0 和γ 进行标定并建立的SDFF
8 # 203.15 171.61 147.49 塑性变形后脆性断裂
模型，称为多温度SDFF模型。该模型在标定参数
9 # 183.15 107.76 93.80 脆性断裂
时仅需进行6次断裂韧性试验，且可以根据断裂试样
的断裂形式灵活选取试验温度，相比原始SDFF模 韧脆转变温度是当累积断裂失效概率为 50%
型不仅减少了至少1/2的试验数量，还简化了试验温 时，标准试样断裂韧度为 100 MPa · m 1/2 所对应的
度的选取和数据处理过程。 温度。通过多温度SDFF模型计算得到0.5T CT试
样和1T CT试样的韧脆转变温度分别为−81 ℃和
2 多温度SDFF模型效果验证
−64 ℃，与试验测得的韧脆转变温度区下平台拐点
2.1 多温度SDFF模型分析 对应的温度吻合良好，相对误差在6%左右。采用
采用文献［29］中的国产RPV A508-III钢单轴 0.5T CT试样试验结果得到的韧脆转变温度较采用
拉伸试验数据，得到临界应变能密度与温度的关系， 1T CT试样得到的更低，说明试样几何尺寸对RPV
如图1所示，拟合得到式（8）中参数α 为30.95， β 为 钢的韧脆转变行为具有一定影响。韧脆转变温度代
0.076。 表着试样的断裂方式由脆性断裂开始向韧性断裂转
114