Page 132 - 机械工程材料2025年第三期

薛 河，等：基于压入响应的异种金属焊接接头材料力学性能计算方法

表1 不同屈服应力下加载曲率和加载指数与应变硬化指数的拟合参数
Table 1 Fitting parameters between loading curvature and loading index and strain hardening index
under different yield stresses

屈服应力/MPa a b d e f
200 112 878.245 −16 291.832 4 258.866 0.584 33 0.976 15
300 117 946.322 −10 037.172 5 162.260 0.579 50 0.988 44
400 117 779.420 −2 563.466 5 871.541 0.578 02 0.996 82
500 123 780.779 −119.329 7 162.056 0.563 19 1.008 83
600 122 757.020 5 428.674 8 150.501 0.551 86 1.020 59

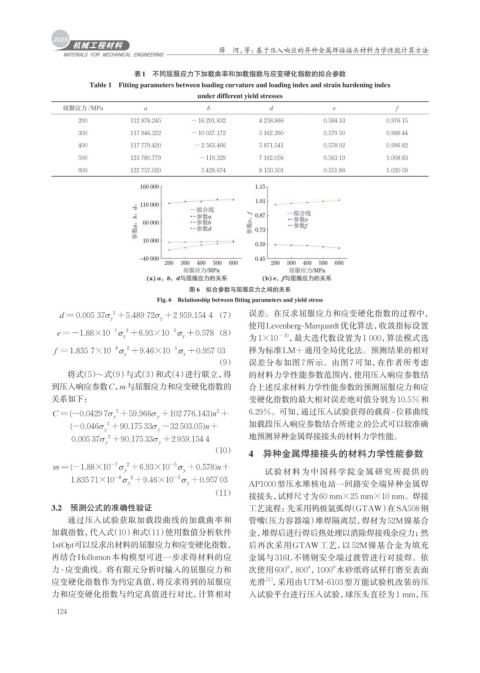
图 6 拟合参数与屈服应力之间的关系
Fig. 6 Relationship between fitting parameters and yield stress
d = 0.005 37 σ y 2 +5.489 72 σ y +2 959.154 4 （7） 误差。在反求屈服应力和应变硬化指数的过程中，
使用Levenberg-Marquardt优化算法，收敛指标设置
（8） −10
为1×10 ，最大迭代数设置为1 000，算法模式选
择为标准LM+通用全局优化法。预测结果的相对
（9） 误差分布如图 7 所示。由图 7 可知，在作者所考虑
将式（5）~式（9）与式（3）和式（4）进行联立，得 的材料力学性能参数范围内，使用压入响应参数结
到压入响应参数C，m与屈服应力和应变硬化指数的 合上述反求材料力学性能参数的预测屈服应力和应
关系如下： 变硬化指数的最大相对误差绝对值分别为10.5%和
C = (-0.0429 7 σ y 2 +59.966 σ y +102 776.143)n 2 + 6.29%。可知，通过压入试验获得的载荷-位移曲线
n
(-0.046 σ y 2 +90.175 33 σ y -32 503.05) + 加载段压入响应参数结合所建立的公式可以较准确
0.005 37 σ y 2 +90.175 33 σ y +2 959.154 4 地预测异种金属焊接接头的材料力学性能。
（10） 4 异种金属焊接接头的材料力学性能参数

试验材料为中国科学院金属研究所提供的
AP1000型压水堆核电站一回路安全端异种金属焊
（11） 接接头，试样尺寸为60 mm×25 mm×10 mm。焊接
3.2 预测公式的准确性验证 工艺流程：先采用钨极氩弧焊（GTAW）在SA508钢
通过压入试验获取加载段曲线的加载曲率和 管嘴（压力容器端）堆焊隔离层，焊材为52M镍基合
加载指数，代入式（10）和式（11）使用数值分析软件 金，堆焊后进行焊后热处理以消除焊接残余应力；然
1stOpt可以反求出材料的屈服应力和应变硬化指数， 后再次采用GTAW工艺，以 52M镍基合金为填充
再结合Hollomon本构模型可进一步求得材料的应 金属与316L不锈钢安全端过渡管进行对接焊。依
#
#
#
力-应变曲线。将有限元分析时输入的屈服应力和 次使用600 ，800 ，1000 水砂纸将试样打磨至表面
［5］
应变硬化指数作为约定真值，将反求得到的屈服应 光滑 ，采用由UTM-6103型万能试验机改装的压
力和应变硬化指数与约定真值进行对比，计算相对 入试验平台进行压入试验，球压头直径为1 mm，压
124