Page 131 - 机械工程材料2025年第三期

薛 河，等：基于压入响应的异种金属焊接接头材料力学性能计算方法

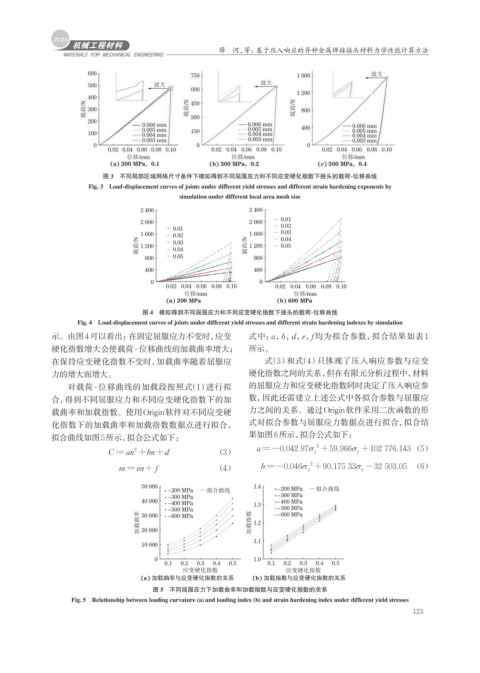
图 3 不同局部区域网格尺寸条件下模拟得到不同屈服应力和不同应变硬化指数下接头的载荷-位移曲线
Fig. 3 Load-displacement curves of joints under different yield stresses and different strain hardening exponents by
simulation under different local area mesh size
2 400 2 400
2 000 2 000 0.01
0.02
0.01
1 600 0.02 1 600 0.03
0.04
载荷/N 1 200 0.03 载荷/N 1 200 0.05
0.04
800 0.05 800
400 400
0 0
0.02 0.04 0.06 0.08 0.10 0.02 0.04 0.06 0.08 0.10
位移/mm 位移/mm
(a) 200 MPa (b) 600 MPa
图 4 模拟得到不同屈服应力和不同应变硬化指数下接头的载荷-位移曲线
Fig. 4 Load-displacement curves of joints under different yield stresses and different strain hardening indexes by simulation
示。由图4可以看出：在固定屈服应力不变时，应变 式中：a，b，d，e，f均为拟合参数，拟合结果如表 1
硬化指数增大会使载荷-位移曲线的加载曲率增大； 所示。
在保持应变硬化指数不变时，加载曲率随着屈服应 式（3）和式（4）只体现了压入响应参数与应变
力的增大而增大。 硬化指数之间的关系，但在有限元分析过程中，材料
对载荷-位移曲线的加载段按照式（1）进行拟 的屈服应力和应变硬化指数同时决定了压入响应参
合，得到不同屈服应力和不同应变硬化指数下的加 数，因此还需建立上述公式中各拟合参数与屈服应
载曲率和加载指数。使用Origin软件对不同应变硬 力之间的关系。通过Origin软件采用二次函数的形
化指数下的加载曲率和加载指数数据点进行拟合， 式对拟合参数与屈服应力数据点进行拟合，拟合结
拟合曲线如图5所示，拟合公式如下： 果如图6所示，拟合公式如下：
= C 2 + an +bn d （3） a =-0.042 97 σ y 2 +59.966 σ y +102 776.143 （5）

= m + en f （4） b =-0.046 σ y 2 +90.175 33 σ y -32 503.05 （6）

50 000 1.4 —
-200 MPa — 拟合曲线 -200 MPa 拟合曲线
-300 MPa -300 MPa
40 000 -400 MPa 1.3 -400 MPa
-500 MPa -500 MPa
加载曲率 20 000 加载指数 1.2
-600 MPa
30 000
-600 MPa
1.1
10 000
0 1.0
0.1 0.2 0.3 0.4 0.5 0.1 0.2 0.3 0.4 0.5
应变硬化指数 应变硬化指数
(a) 加载曲率与应变硬化指数的关系 (b) 加载指数与应变硬化指数的关系
图 5 不同屈服应力下加载曲率和加载指数与应变硬化指数的关系
Fig. 5 Relationship between loading curvature (a) and loading index (b) and strain hardening index under different yield stresses
123