Page 118 - 机械工程材料2025年第三期

李洋阳，等：双金属复合管中L360MS管线钢焊接接头的疲劳裂纹扩展行为以及疲劳寿命预测

da
lg =lgCn ∆ （7）
+ lg K
dN
对不同试样的da/dN与∆K进行线性回归，即
可获得材料常数C和n值。不同试样的da/dN-∆K
关系曲线如图11所示，所得材料常数和相关系数如
表 3 所示。由表 3 可以看出，在同一应力比 0.1 下，
L360MS管线钢焊接接头不同试样的材料常数C不
在同一数量级上，说明母材、HAZ、焊缝的疲劳裂纹
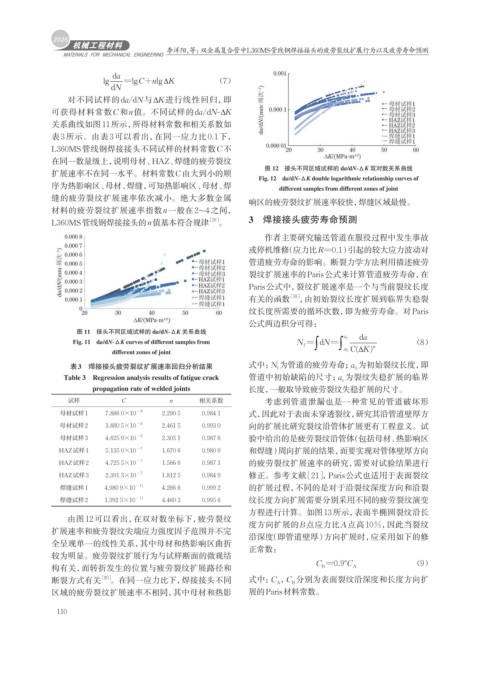
图 12 接头不同区域试样的 da/dN-ΔK 双对数关系曲线
扩展速率不在同一水平。材料常数C由大到小的顺
Fig. 12 da/dN-ΔK double logarithmic relationship curves of
序为热影响区、母材、焊缝，可知热影响区、母材、焊 different samples from different zones of joint
缝的疲劳裂纹扩展速率依次减小。绝大多数金属
响区的疲劳裂纹扩展速率较快，焊缝区域最慢。
材料的疲劳裂纹扩展速率指数n一般在2~4之间，
L360MS管线钢焊接接头的n值基本符合规律 ［19］ 。 3 焊接接头疲劳寿命预测
作者主要研究输送管道在服役过程中发生事故
或停机维修（应力比R=0.1）引起的较大应力波动对
管道疲劳寿命的影响。断裂力学方法利用描述疲劳
裂纹扩展速率的Paris公式来计算管道疲劳寿命，在
Paris公式中，裂纹扩展速率是一个与当前裂纹长度
有关的函数 ［18］ ，由初始裂纹长度扩展到临界失稳裂
纹长度所需要的循环次数，即为疲劳寿命。对Paris
公式两边积分可得：
图 11 接头不同区域试样的 da/dN-ΔK 关系曲线
∫
N
Fig. 11 da/dN-ΔK curves of different samples from N =d = ∫ c a da （8）
different zones of joint f a 0 C( K∆ ) n
表3 焊接接头疲劳裂纹扩展速率回归分析结果 式中：N 为管道的疲劳寿命；a 为初始裂纹长度，即
f
0
Table 3 Regression analysis results of fatigue crack 管道中初始缺陷的尺寸；a 为裂纹失稳扩展的临界
c
propagation rate of welded joints 长度，一般取导致疲劳裂纹失稳扩展的尺寸。
试样 C n 相关系数 考虑到管道泄漏也是一种常见的管道破坏形
−8
母材试样1 7.886 0×10 2.290 5 0.984 1 式，因此对于表面未穿透裂纹，研究其沿管道壁厚方
−8
母材试样2 3.880 5×10 2.461 5 0.993 0 向的扩展比研究裂纹沿管体扩展更有工程意义。试
母材试样3 4.625 9×10 −8 2.305 1 0.987 6 验中给出的是疲劳裂纹沿管体（包括母材、热影响区
HAZ试样1 5.135 0×10 −7 1.670 6 0.980 9 和焊缝）周向扩展的结果，而要实现对管体壁厚方向
HAZ试样2 4.725 5×10 −7 1.586 6 0.987 1 的疲劳裂纹扩展速率的研究，需要对试验结果进行
HAZ试样3 2.391 3×10 −7 1.812 5 0.984 9 修正。参考文献［21］，Paris公式也适用于表面裂纹
−11
焊缝试样1 4.980 9×10 4.286 8 0.999 2 的扩展过程，不同的是对于沿裂纹深度方向和沿裂
−11
焊缝试样2 1.992 5×10 4.460 3 0.995 6 纹长度方向扩展需要分别采用不同的疲劳裂纹演变
方程进行计算。如图13所示，表面半椭圆裂纹沿长
由图12可以看出，在双对数坐标下，疲劳裂纹
度方向扩展的B点应力比A点高10%，因此当裂纹
扩展速率和疲劳裂纹尖端应力强度因子范围并不完
沿深度（即管道壁厚）方向扩展时，应采用如下的修
全呈现单一的线性关系，其中母材和热影响区曲折
正常数：
较为明显。疲劳裂纹扩展行为与试样断面的微观结
C =0.9 C （9）
n
构有关，而转折发生的位置与疲劳裂纹扩展路径和 B A
断裂方式有关 ［20］ 。在同一应力比下，焊接接头不同 式中：C ，C 分别为表面裂纹沿深度和长度方向扩
A
B
区域的疲劳裂纹扩展速率不相同，其中母材和热影 展的Paris材料常数。
110